A ‘thought experiment’ called The Dome published in 2003, claims that Newtonian physics can be shown to be non-deterministic. Shocking, huh? Not really. Mathematical singularities crop up all the time in physics and represent points where the model breaks down. We handle this by excluding them.

Newton’s laws are deterministic, but they’re not complete.

My initial reaction to Norton’s Dome was quite disparaging because his non-deterministic ‘solution’ is so antithetical to anything a physicist would construct. It jumps out as immediately wrong. However, I’ve learned a great deal from thinking about it. It contains several surprises. What more can we ask of a thought experiment? I’ve come to think it’s a little gem.

Norton’s Dome

Norton deserves credit for constructing such a clever set-up. It hides from sight – in the attic of higher order differential forms – what would otherwise be a perfectly obvious flaw. We’ll take this error down and dust it off in plain view in a simpler but equivalent form to expose it. The dome also turns out to have some very interesting mathematical (geometric) properties which have proven to be very effective red-herrings.

Imagine a dome of a certain shape which is perfectly symmetrical. Atop the dome, sitting at the precise vertex sits a point-like mass (represented by a sphere in the drawing so we can see it). The surface is perfectly slippery (no friction forces). The only force acting on the mass is gravity and the dome is fixed and unmovable.

The shape of the dome is given by the equation in the diagram.

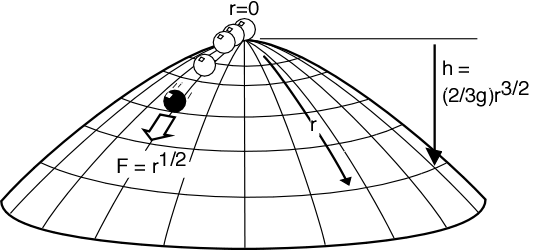
Since gravity is the only force acting, it can only push the particle in a direction if the particle is somewhere other than the apex. At the apex, the force from the dome goes straight up, is equal an opposite to , so the particle doesn’t move at all. Everywhere else, the force is at the angle of the dome’s surface and so a fraction of will be sideways. Note that is measured down from zero at the top of the dome, and is the length of the arc along the curve from the apex to the point, and not the horizontal distance from the apex.

Norton’s set up is somewhat cavalier and needs some fixes, but none are fatal to his argument and so we’ll fix them in a bit just to clear them out of way. But first, let’s get into the problem as he argues it.

The radial force on the particle – that is the force in the direction along the dome’s surface away from the apex – is given, according to Norton, by:

(If you’re a physicist you may be cringing at several problems already but bear with…)

Now, from Newton we know , which along the arc is:

 

We can set the mass to 1 for simplicity, and so:

 

Clearly at the apex, , there is no force, no acceleration and the particle stays still, so and this is obviously the trivial solution to the above equality.

This is where Norton gets tricky with us. He posits another solution to the equation above, where, for some arbitrary time, :

It’s easy to check that both parts of this function are correct solutions. You can differentiate the solution twice and check if you feel like it. We’re expected to accept them both as Newtonian. It seems that way, right? because they’re solutions, but in fact the top equation is not Newtonian at the apex (clearly since it moves despite the absence of a force there).

Norton however, having stitched this monster up, interprets it as meaning that the particle can simply start shooting off down the dome’s side after an arbitrary time and with no apparent cause.

This is baffling. It’s bizarre to stitch two different solutions to an equation together using an arbitrarily chosen boundary and then claim it still represents something physical.

Norton, however, starts referring to time  as the ‘excitation’ time, attempting to slap some physics-esque linguistic make-up on his Frankenstein creation to try to pass it off.

I will get round to showing just how absurd and unphysical it is to stitch solutions together in this way, but first we need to fix up the problem statement and also dig deeper. Where did this other solution come from? What does it represent?

There are various additional issues that are unphysical which could be distractions. We want our vision as clear as possible, but also this dome shape turns out to be a great deal more interesting than it first looks!

Let’s get physical!

1) Dimensions

You may noticed the equation for the height of the dome has the wrong dimensions. It should have dimensions of length () but instead has . This is easily fixed with a constant factor, , with dimension of . Since we can set this constant to 1 this is a little pernickety but best have it out the way.

2) Infinite force?

Gravity is the only force acting, and yet somehow we’ve ended up with a force equation that scales unbounded as the square root of . The maximum force the particle can experience is which coincides with the dome surface being vertical. So how on earth have we ended up with the force scaling unbounded as the square root of the arc length?

It could easily sneak past the casual reader that the surface described the equation isn’t physically possible over all . This is very easy to miss because we’re shown a mixed coordinate system which is looks Cartesian, but in fact isn’t.

If we had been given a curve expression in terms of and we could more easily see where the curve behaves strangely, but he’s given an unusual one mixing the arc length with height which hides some very bad behaviour:

As increases, there comes a point where the height (or rather depth) equals and then exceeds the length of the arc!

Take a moment to think about that.

The length of an arc of a curve is always going to be longer than its depth or width. It can equal either – if it happens to be a straight line – but how can an arc ever that started out longer become shorter in total length than its height? There is no curve we can draw where the arc length is less than its height:

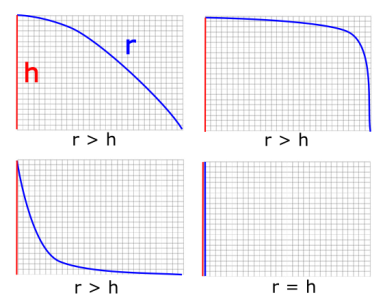
The only case where it can even equal the height is is the case where it drops straight down. Yet the curve equation we’ve been describes a shape whose depth rapidly starts to exceeds its arc length. Clearly this isn’t physically possible without bending space itself. An interestingly shaped dome indeed!

We must impose a constraint on the dome equation to stop this. The rate of change of the height can never be allowed to exceed the rate of change of the arc length. We can express this geometric constraint as:

which gives us

or

This is fine. So long as our dome is cut off before this point, then at least it’s physically possible.

Norton doesn’t appear to have noticed or at least doesn’t point out the pathological nature of his dome’s surface but it doesn’t matter as we only need to consider the dome near the apex anyway.

(The curve also turns out to be pathological at the apex in a far less obvious way, and some have focused on this as the flaw in his argument. It’s interesting but we don’t need go into complex mathematical arguments about Guassian curvature or Lipschitz continuity to dispatch this monster.)

Frankenstein’s Equation

Okay, so given that the two equations Norton has supplied are easily shown to be correct solutions to the equation, why is his stitched-together version of them flawed?

Being a valid mathematical solution to the equation isn’t enough to ensure we have a valid physical model. This will become very obvious in a moment but first we need to see that the two equations differ in a very important respect. The both represent different physical solutions. One is the motionless particle, but what does the other solution physically represent?

Well, it’s one of the many possible “equations of motion” for a particle on this Dome’s surface. In this case, it happens to describe a trajectory passing through the apex. This is the first clue that this is a non-Newtonian solution: it describes the particle sliding off the apex despite it having zero velocity and zero acceleration there!

If we look at negative time, it also describes the particle shooting up the curve up, over and through the apex. The point when the particle is exactly on the apex is when and you can see that becomes zero.

The inclusion of T in the equation here is a red-herring. All it does is offset the moment when the particle passes through the apex. If it’s 4, then the particle will be at the apex when .  Remember we don’t have to start at time zero, since the choice of what to call zero is arbitrary. Negative times are just as valid here, and they just describe the particle’s motion before the time we arbitrarily called zero.

We can calculate the velocity of the particle easily enough, just by differentiating with respect to time:

This tells us that at time , the velocity is zero too.

Now, at first this might be surprising. If the velocity is zero and the position is zero at time ‘zero’ (i.e. ), then how come this solution shows the particle moving at all other times? How does it ever get off the apex once it’s there? If no there’s no acceleration or force at the apex, and the particle has zero velocity there, then how can it possibly move away?

First, let’s confirm the acceleration is zero by differentiating again:

This is also zero at time , which we expected since we set up the whole system this way.

So it’s true that the acceleration and velocity is zero at this one instant in time but they are not the whole picture. If we keep differentiating, we can see that the rate of change of acceleration (called ‘jerk’) is zero too:

But if we differentiate one more time to get the rate of change of the jerk (sometimes called snap, or jounce) we’re in for a surprise, because we see immediately that this is non-zero at all times:

Jounce, or snap, is the ‘acceleration of acceleration’.  It’s perfectly reasonable for it to be non-zero in real physical situations (fun fact: jerk and snap are quite important considerations when designing roller coasters), but in a real, complex system its value would come from a complex interplay of forces and structures.

According to this (mathematically correct) solution to the differential equation, the particle acquires acceleration at an accelerating rate at all times and positions on the dome.

So is this solution Newtonian? I don’t see how since it violates the Newton’s first law:

Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.

“An object at rest will remain at rest unless acted upon by an external and unbalanced force. An object in motion will remain in motion unless acted upon by an external and unbalanced force.”

Implicit in this statement is that if the force is zero, then all higher orders of the force must also be zero to ensure the acceleration, despite being zero, isn’t changing.

This raises deep questions about how we want our model particles to behave in this unusual condition. Should the particle move? If we want to preserve time-symmetry then answer is yes. If we want to strictly preserve Newton’s laws the answer is no.

Conservation of Energy

Just because we have an equation that is the solution to a differential equation does not mean that it represents something physical over its entire range. Just as the dome equation becomes physically meaningless beyond a certain apex length, Norton’s motion equation isn’t valid over its full range. It describes a path that fits a mathematical constraint but that path does not, in fact, match the expected trajectory of the particle.

Physics cares about maths, maths really doesn’t care about physics.

We must make it care, by applying appropriate constraints and conditions wherever we notice it no longer represents something physical.

For example, at first glance it would appear that energy is conserved over the whole path. We can calculate the drop in potential energy for the particle at any point on the dome surface, and we can calculate the (apparent) kinetic energy at that point and they appear to match, but if we consider the complete drop energy is not actually conserved:

The force in the horizontal direction is always positive. This rises from zero at the start, and reaches a maximum as the particle slides past the point where the component is more down than sideways (a dome angle of 45 degrees). After this point the particle continues to accelerate horizontally but that acceleration decreases. The horizontal kinetic energy reach some positive maximum value.

According to Norton’s equation though, the value for kinetic energy at , where the dome ends, is exactly equal to the drop in potential:

The velocity described by the equation of motion however is entirely in the vertical direction at this point on the curve and therefore this only represents the particle’s vertical kinetic energy. If we add the positive value for the horizontal kinetic energy, where did this extra energy come from? The curve violates a fundamental conservation law.

The particle would actually fly off the dome at some point because the dome drops away faster than a freefall parabola. If we wanted to we could work out the precise moment where this happens.

A stitch in time…

…violates casuality.

An equation of motion with a constant value for snap is still deterministic, even if it isn’t Newtonian. So where does the apparent non-deterministic nature come from?

Consider that the two equations represent different particles. One is a stable solution of the particle being at apex over all time. The other is an unstable particle which reaches the apex and leaves again. It’s not appropriate to combine these into a single equation since they don’t share the same state at the apex.

The particle suddenly starts behaving non-deterministically at time because that’s the arbitrarily chosen point at which we ‘switch particles’.

We would never stitch two independent solutions together with different initial conditions since there’s no physical justification for this change of state.

Consider a much simpler case:

On a perfectly flat surface with zero friction, the horizontal force is always zero. The valid solutions to the equations of motion include the particle at rest:

and the particle moving at a constant velocity:

where is arbitrary. These are both correct solutions (the latter being a generalisation of the first). Both of these solutions are perfectly Newtonian but they represent two different particles.

Can we stitch them together at an arbitrary time ?

No, of course we can’t. Why? Because they have different initial conditions. Let’s say the velocity :

	Newton / still	Newton / constant v
position	0	0
velocity	0	50
acceleration	0	0

If we attempt to do this, we get an equally absurd non-physical and non-deterministic result in which the particle appears to suddenly move off at time T, in the absence of a physical cause.

Equally, it makes no physical sense to stitch these two piecewise together:

	Newtonian / Stable	Unstable / non-Newtonian
position	0	0
velocity	0	0
acceleration	0	0
jerk	0	0
snap/jounce	0	1/6

It is the stitch in time of two unrelated solutions with different initial values for snap that causes the apparent violation of causality.

What’s fascinating about this is that the equation for motion tells us that to fully describe the state of a particle, we need more than position, velocity and acceleration.

We have two possible particles: one is stable and remains in place at the apex. The other is the class of unstable particles which slide up to/down from the apex. [Note this is a class because snap is a vector. It has a fixed value but can be any orientation.  If we fix the orientation, then our model is back to representing one particle again and is fully deterministic (if not ‘Newtonian’).]

To remain Newtonian and preserve determinism, we can exclude the singular point by constraining the higher orders to zero whenever the net force is zero. We lose time symmetry for this special case if we do this. If we wish to keep that, then we have to accept that Newtonian mechanics is incomplete and consider higher order differentials.

Either of these approaches preserves determinism.

Curvature pathologies and red-herrings

I mentioned early that the dome curve had two red-herring properties.

The first was that it becomes “non-physical” beyond the point at which the curvature is vertical. This is hard to spot in the form given, but in Cartesian coordinates there are no (real) solutions to the equation past this boundary.

The second pathology is more mathematical but occurs at the apex itself where the curve has a singularity in its second order curvature. This has no bearing on the non-deterministic interpretation of Norton’s thought experiment, but it looks suspicious and so some people have fixated on it. It’s probably particularly beguiling the more mathematical training one has had, but I don’t think – as a physicist – it presents any special problems at all. We can reproduce the problem on a perfectly smooth curve easily.

The square root in Norton’s differential equation makes the other motion solution easy to intuit, but so long as we remember to all appropriate constraints we can banish that at the singular point of the apex.

David Malament has done an excellent treatment here, which is well worth a read. Overall this is a very insightful analysis though he incorrectly concludes the non-determinism is a result of the fact the Dome is not Lipschitz continuous.

Any potential with a singular maximum – smooth or otherwise – will have infinite solutions at the apex.

Nonetheless, Malament’s analysis is extremely thorough and adds an extra layer of richness to Norton’s Dome that I think it elevates its worth enormously.

Cartesian Equation for Norton’s Dome

Given the pathological behaviour of Norton’s Dome equation, I was curious to know what it actually looks like. No-one has drawn it accurately, not even Norton himself, which I found interesting.

We need to convert the curve from a relationship between the arc length and the height, to one between the Cartesian x and y coordinates. This is pretty straightforward to with some basic calculus. I’ll skip most of steps because the equations get rather messy in Cartesian coordinates, but by all means verify the in between steps yourself.

I’m going switch symbols, and use a more standard for the vertical position as for the arc length. The curve is rotationally symmetric around the origin so we can work in 2D without losing anything:

To get a relationship for x, we just have to express in known terms and then integrate it over the region. Pythagoras gives us:

 

re-express in terms we can substitute:

 

we know

 

so substituting that and then integrating, we get:

to find C we just apply , and then re-express in terms of , which yields

Not pretty, but it’s plottable, so long as we stay in the valid domain. We can see the exact point where it goes vertical and that’s the farthest point the equation makes sense anyway.

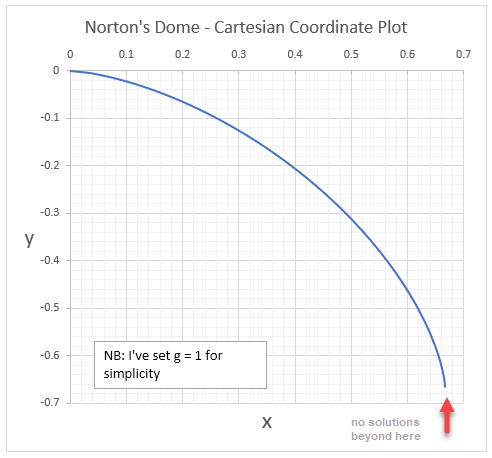
Other Red Herrings

Norton’s original article considers a time-reversed version of his particle which instead arrives at the apex. I’m not entirely sure why, but he discusses a trajectory which takes infinite time for the particle to reach the apex. This has nothing to do with the trajectory described by his solution which is trivially be shown to reach the apex in finite time – (assuming we stay within the well-behaved bounds of the dome equation).

If we start at an arc length of 1/144 for example, it will run up the dome and arrive at the apex in 1 second. As we’ve seen, it has zero velocity and zero acceleration at this point, but moves off after anyway because it still has a positive value for snap.

Implications for Causality: none

Physical models are like maps, small, imperfect representations of something much larger. When we see a crease or fold on a map we don’t expect to see the terrain share the same feature.

It seems ridiculous to me that anyone would try to infer something about reality from the failure of a model. The domains where models fail say nothing about reality. They say only something about the model.

Smooth domes are just as badly behaved…

Consider any smooth dome shape with a singular apex.  Now consider a particle a little way down the side. If we give that particle exactly the kinetic energy needed to reach the apex and point it there, what happens when it reaches the apex?

According to Newton, the particle should stop in the absence of any net force, but as we’ve learned, Newton’s description isn’t complete. Time-reversibility tells us the particle continues to move. Equations of motion are always time-reversible, so the equation will be symmetric around t = 0. The particle must therefore either fall back down again or go over the other side. What’s wonderful about this version of the thought experiment is that we don’t even need to do any maths to see this is true!

It tells us two things:

1. A particle won’t stay at the summit unless it started there, and
2. Newton’s laws cannot be complete

If we think about particles’ states, and consider higher orders like jounce, snap, crackle and pop. (and all the way to infinity), we can see that the choice of path of unstable particles is fully determined by their values, so this isn’t evidence for indeterminism, it is evidence for incompletion.

Indeterminism is merely a consequence of ignoring these and stitching equations together that don’t actually represent the same particle or path. It is a failure to apply the model correctly.

I think this is beautiful and stunning result for a thought experiment.

The same holds for any classical setup. Consider two positive charges fixed in space separated by a short distance. We can place an electron somewhere on the line between them it will feel an electric force. At the precise centre will be zero net force, either side, the electron will feel a force attracting it to the closest positive charge.

The electric potential has a maximum in the centre so this is an unstable equilibrium too. If we we shoot an electron with precisely the right energy it will travel to the centre and, despite no net force move back again (or through) in a time-symmetric manner, once again proving the classical description incomplete.

A generalised result

We don’t even need to consider a specific shape or physical set-up to arrive at this conclusion. Norton’s dome has suggested an entire class of equations of motion which show classical physics to be incomplete.

We see the same results for any equation of motion that is:

1. time-symmetric around
2. polynomial form of order 

We could consider these for example, without even caring what physical system they happen to be solutions for:

Position, velocity and acceleration will be zero at  for every equation of polynomial form of order 3 and above, but non zero everywhere else. Particles following these trajectories move to and from an unstable equilibrium where Newton’s laws fail to be fully descriptive at the singular point where the implied force is zero.